AI810 Blog Post (20243313)

Function-space generative modeling offers a resolution-free and geometrically flexible approach to data generation by treating data as infinite-dimensional functions rather than fixed-dimensional vectors. When applied to molecular conformer generation, this framework enables modeling of 3D molecular structures as smooth fields over graph domains. Recent advances have extended diffusion and Schrödinger Bridge (SB) models into function space, allowing principled interpolation between data distributions. Notably, these methods support unpaired generation and conditioning on informative priors—e.g., initializing with RDKit geometries—improving sample quality in structured domains. However, molecules pose unique challenges due to their graph-specific Laplacians, which yield distinct eigenbases for each sample, complicating coherent simulation and transfer. This work outlines the theoretical foundation of infinite-dimensional SDEs, highlights recent progress in function-space molecular generation, and identifies key limitations and future directions—particularly the need for shared or learnable spectral embeddings to enable scalable and generalizable SB-based generative models for molecules.

Introduction

Why Introduce Generative Modeling in Function Space?

Traditional generative models typically represent data as finite-dimensional vectors, such as pixels for images or Cartesian coordinates for molecular conformations. While effective for certain tasks, this discrete representation inherently constrains the models’ flexibility, resolution, and generalizability. For example, images are typically generated at fixed resolutions, limiting their use at arbitrary scales. Similarly, molecules represented explicitly by atomic coordinates suffer from limited resolution and sensitivity to permutation and alignment, complicating applications in molecular simulations and drug design.

Image as function .

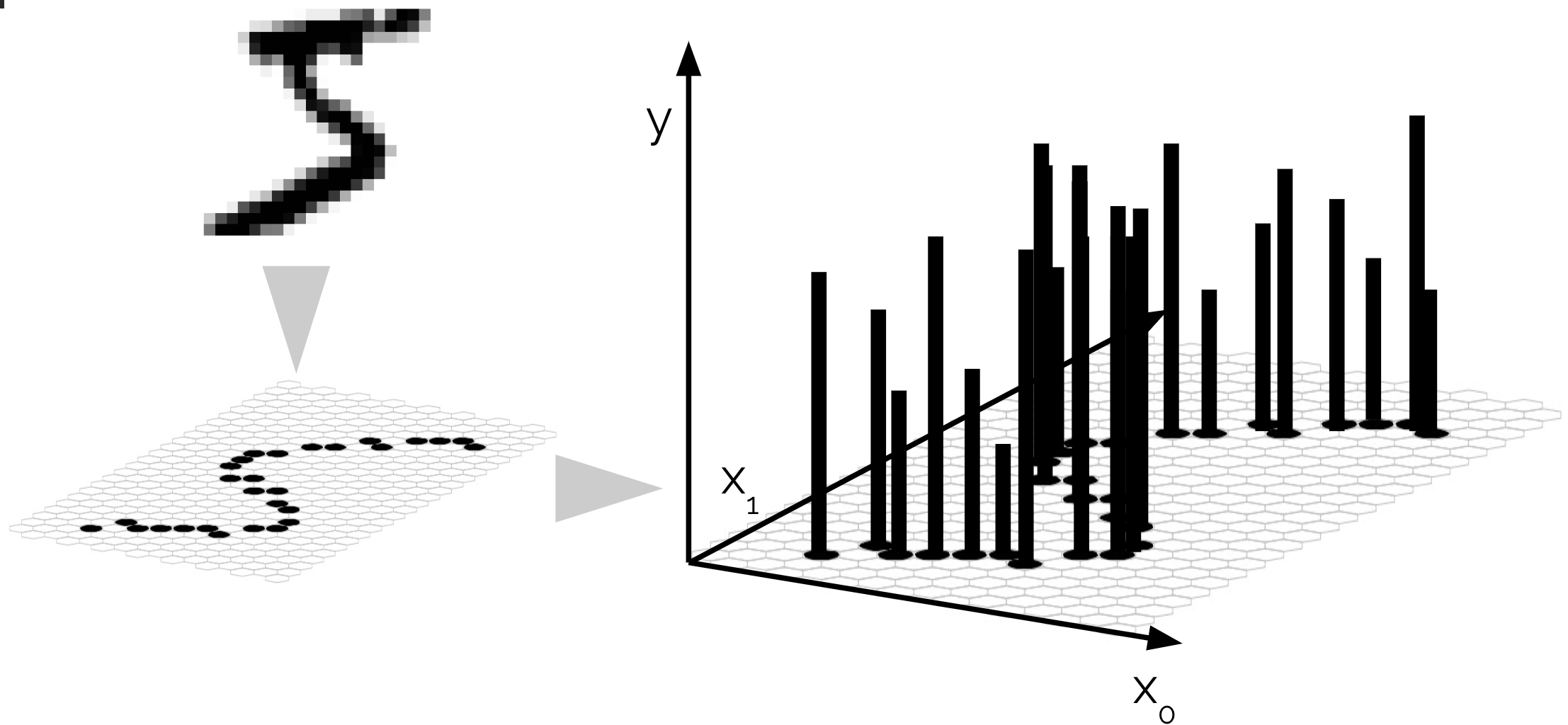
Generative modeling in \emph{function space} addresses these intrinsic limitations by treating data as infinite-dimensional functions rather than fixed-dimensional vectors. Specifically, data instances—such as images, time-series, or molecular conformations—can be conceptualized as continuous functions mapping input coordinates (spatial or structural) into output spaces (such as colors for images or three-dimensional positions for molecules). Formally, an image can be represented as a function $f:\mathbb{R}^2\rightarrow\mathbb{R}^3$, mapping any location in two-dimensional space directly to RGB values. Analogously, a molecular structure can be treated as a function that maps vertices of a molecular graph into spatial coordinates, i.e., $f:V(G)\rightarrow\mathbb{R}^3$.

This functional representation provides several compelling advantages:

Resolution invariance: A single trained model can generate outputs at arbitrary resolutions, overcoming the limitation of discrete grid-based methods.
Permutation invariance and continuity: By inherently encoding permutation invariance, function space models avoid explicit symmetrization procedures, which can be computationally expensive or impractical for large datasets, especially in molecular contexts.
Natural interpolation and extrapolation: Functional representations facilitate straightforward interpolation and extrapolation within the generative model’s learned function space, enhancing the generalizability of generated outputs.
Robustness to sampling strategies: Since functions can be evaluated continuously, generative models are robust to various sampling schemes, enabling efficient and flexible deployment in diverse settings.

The adoption of function space modeling, especially in complex domains such as molecular generation, has been facilitated by recent advances in machine learning frameworks adept at managing infinite-dimensional inputs and outputs, including neural operators, Gaussian processes, and diffusion processes. In this post, we discuss how the infinite-dimensional framework can be extended specifically for molecular generation, and we outline the key challenges involved in this adaptation.

Infinite-dimensional SDEs

In traditional finite-dimensional settings, a stochastic differential equation (SDE) in $\mathbb{R}^d$ is typically expressed as: $\begin{equation} dX_t = f(t,X_t)\,dt + \sigma(t,X_t)\,dW_t, \end{equation}$

where $W_t$ is a standard Wiener process. Extending this formulation to infinite-dimensional spaces involves defining SDEs in Hilbert spaces :

\[\begin{equation} dX_t = AX_t\,dt + \sigma\,dW_t^Q,\quad X_0 \in H, \end{equation}\]

where:

$H$ is an infinite-dimensional Hilbert space,
$A : H \to H$ is typically an unbounded linear operator,
$W_t^Q$ is a $Q$-Wiener process, a generalization of the finite-dimensional Wiener process with covariance operator $Q$ reflecting spatial correlations inherent in infinite-dimensional spaces.

Specifically, a $Q$-Wiener process can be expanded via an eigenbasis of the Hilbert space $H$:

\[\begin{equation} W_t^Q = \sum_{k=1}^{\infty} Q^{1/2}\phi_k\, w_t^{(k)}, \end{equation}\]

where $\{\phi_k\}$ forms an orthonormal basis of $H$ and $w_t^{(k)}$ are independent scalar Wiener processes. The covariance operator $Q$ determines spatial correlation and smoothness properties of the stochastic process. Unlike finite-dimensional spaces where identity covariance operators suffice, in infinite-dimensional spaces, the identity operator is typically not trace-class, necessitating a carefully chosen covariance operator $Q$ to ensure mathematical and physical relevance.

Role of $Q$: The covariance operator $Q$ plays a crucial theoretical role in infinite-dimensional SDEs by ensuring the stochastic increments have finite trace and appropriately reflect spatial correlations. It defines the regularity and correlation structure of the infinite-dimensional noise, making $Q$ essential for well-posedness and tractability of the SDE in infinite-dimensional spaces.

To numerically simulate infinite-dimensional SDEs, particularly those driven by negative Laplacian operators $-\Delta$, one often employs spectral decompositions. Specifically, for a two-dimensional domain $x = (x_1, x_2) \in \mathbb{R}^2$, eigenfunctions $\phi^{(k)}(x)$ and eigenvalues $\lambda^{(k)}$ of $-\Delta$ under zero Neumann boundary conditions satisfy:

\[\begin{equation} -\Delta \phi^{(k)}(\mathbf{x}) = \lambda^{(k)} \phi^{(k)}(\mathbf{x}), \quad \frac{\partial \phi^{(k)}(\mathbf{x})}{\partial x_1} = \frac{\partial \phi^{(k)}(\mathbf{x})}{\partial x_2} = 0. \end{equation}\]

On a rectangular domain, these eigenfunctions form a separable cosine basis:

\[\begin{equation} \phi^{(n, m)}(x_1, x_2) \sim \cos{\left(\frac{\pi n x_1}{W}\right)}\cos{\left(\frac{\pi m x_2}{H}\right)}, \quad \lambda^{(n, m)} = \pi^2 \left(\frac{n^2}{W^2} + \frac{m^2}{H^2} \right). \end{equation}\]

Thus, the negative Laplacian operator $-\Delta$ can be represented via eigen-decomposition:

\[\begin{equation} -\Delta = E D E^{\top} \end{equation}\]

where $E^{\top}$ corresponds to the discrete cosine transform (DCT) projection matrix, i.e., $\tilde{X}_t = E^{\top} X_t = \text{DCT}(X_t)$, and $D$ is diagonal containing eigenvalues. The covariance matrix $Q$ crucially characterizes the spatial correlation and numerical stability in simulations.

Infinite-dimensional Diffusion Models

Generated Image (function) .

Many classical finite-dimensional diffusion models can naturally and successfully be extended into infinite-dimensional or function spaces . These infinite-dimensional diffusion models leverage the theoretical framework of infinite-dimensional SDEs, enabling direct modeling of distributions on functional data (e.g., images, molecular structures, and continuous time-series). This extension provides resolution invariance, enhanced flexibility, and robust generative capabilities beyond traditional finite-dimensional frameworks.

While standard diffusion models typically generate data by transforming Gaussian noise through a learned score or drift function, a natural generalization arises when we consider generating data conditioned on data—leading to the framework of Schrödinger Bridge problems. In this formulation, one seeks a diffusion process that connects two data distributions (e.g., source and target) while remaining close to a reference process in KL divergence. This generalization has led to recent developments in data-to-data generative models, and crucially, when it meets the infinite-dimensional generalization, it enables resolution-free unpaired generation across diverse modalities.

Results on Unpaired image transfer task.

Red boxed images were upsampled (using bi-linear transformation) from the observed resolution.

Infinite-Dimensional Molecule Conformal Generation

Recent work byintroduces a principled framework for molecular conformer generation in function space by leveraging spectral methods defined over molecular graphs. The key insight is that a molecular conformer—the 3D arrangement of atoms in a molecule—can be represented as a smooth function over the molecular graph. To be specific, Let $G=(V,E)$ be the molecular graph with $n$ atoms, and let $:$ be its graph (symmetric) Laplacian. Owing to he symmetry of $L$, its eigenvectors $\{\phi_k\}_{k=1}^n$ form an orthonormal basis of $\mathbb{R}^n$. Any molecular conformation $X \in \mathbb{R}^{n \times 3}$ (i.e., positions of $n$ atoms in 3D space) can be decomposed as follows:

\[\begin{equation} X = \sum_{k=1}^n c_k \phi_k, \quad \text{with}\; c_k \in \mathbb{R}^{1 \times 3} \end{equation}\]

where each coefficient $c_k$ captures the projection of the molecular geometry onto the $k$-th graph harmonic. This decomposition allows modeling conformers in the frequency domain rather than Cartesian coordinates. This spectral parameterization enables generative models to operate on coefficients ${c_k}$, which typically exhibit spatial smoothness and decay, allowing for compact representations. Furthermore, the conformer can be generated in function space via a diffusion process over these coefficients. This formulation enables the application of infinite-dimensional generative models and Schrödinger Bridge methods in graph-based domains. Importantly, since the graph Laplacian is molecule-specific, each sample is embedded in its own basis. Addressing this heterogeneity remains a key challenge for extending function-space models to general molecular datasets.

Drug generation Traj.

SB with informative priors and continuous conformers. The Schr”odinger Bridge (SB). framework allows generation from an initial distribution to a target distribution while remaining close to a reference process. Traditionally, generative models using SB or diffusion start from pure noise; however, this may be suboptimal in structured domains like molecular conformers. A more informative prior can improve generation quality and convergence. For instance, initialize the generation with conformers produced by RDKit, enabling a guided generation path that improves sample quality and optimization. This strategy suggests that SB methods can generalize such priors in a principled way, bridging between known or heuristically sampled initial configurations and optimized final geometries.

Moreover, function-space formulations naturally extend this idea by representing conformers not as fixed atom positions, but as fields over the molecular graph. For example, show that continuous evaluation of conformers is possible by interpolating eigenfunction representations. For a point $p$ along a bond between atoms $v_i$ and $v_j$, the representation is interpolated as:

$\begin{equation} \phi(p) = \alpha \phi(v_i) _ (1-\alpha) \phi(v_j), \quad \alpha \in [0, 1], \end{equation}$ and the model maps $\phi(p)$ to a 3D coordinate. This enables continuous evaluation of conformers across the molecular graph, even at locations not seen during training.

This formulation not only confirms the flexibility of the field-based approach, but also indicates potential extensions toward richer physical modeling. For example, if the input includes electronic density estimates or quantum observables (e.g., from QMC methods), the model may predict physically meaningful fields beyond atomic coordinates. These directions remain speculative but open compelling future paths for conformer field learning and molecule-level Schr”odinger Bridge extensions.

Practical Limitation. Despite these promising advances, there are key limitations when applying function-space SB to molecular data. The central issue lies in the fact that each molecular graph defines its own graph Laplacian, and consequently, its own eigenbasis. This means that molecular conformers are embedded in non-aligned spectral coordinates across different samples. To apply simulation techniques (e.g., diffusion or SB in coefficient space), one would ideally need a shared basis across the dataset—but aligning or transferring conformers between mismatched bases is fundamentally ill-posed or at least highly nontrivial.

One workaround is to embed all molecules into a fixed-size global basis (e.g., using graph matching or kernelized embeddings), but such methods risk losing molecule-specific structural information. This highlights a tension: while infinite-dimensional modeling leverages smoothness and resolution-free behavior, its assumptions clash with the heterogeneity of molecular graph structures. Bridging this gap—through universal spectral embeddings, learned graph bases, or implicit function representations—remains a crucial open challenge for scalable and generalizable molecular generative models.

Concluding remarks

Function-space generative modeling provides a powerful and principled framework for modeling structured data, enabling resolution-free, smooth, and domain-aware generation. By casting data as continuous functions over space or graphs, these models unify interpolation, uncertainty quantification, and conditioning into a single representation. This approach has shown strong potential across regular domains like images and continuous time-series, and more recently, irregular domains like molecular graphs.

However, applying infinite-dimensional Schr”odinger Bridge (SB) formulations to molecular conformer generation introduces unique challenges due to the graph-specific spectral decompositions. Unlike regular grids, molecular graphs do not share a common coordinate system, making model transferability and simulation coherence nontrivial. Recent works such as and have made substantial progress by exploiting informative priors and leveraging interpolable eigenfunctions, but general-purpose, scalable solutions remain elusive.

Going forward, overcoming the mismatch of graph-specific eigenbases, incorporating physical constraints like bond flexibility or quantum observables, and developing architectures that natively handle variable graph topologies will be key. Combining these insights with the expressive power of SB and function-space modeling could lead to a new generation of molecular generative models that are not only accurate, but also chemically meaningful, generalizable, and physically grounded.